Please switch off AdBlock for this webside to display it correctly (there are no ads here).
Truncated Lorentzian peak
modelname
TruncatedLorentz|TruncatedLorentzianPeak|TLP
Imaginary part of complex dielectric function is described by five parameters \(E_{\rm g}\), \(E_{\rm h}\), \(N_1\), \(E_1\), \(B_1\):
$$
\begin{array}{lcl} \displaystyle
\varepsilon_{\rm i} = \frac{N_1 (E-E_{\rm g})^2 (E-E_{\rm h})^2}{{\cal C}_{\rm N} E^2 \left((E-E_1)^2+B_1^2/4\right)} & \mbox{for} & E_{\rm h} > E > E_{\rm g} \\
\varepsilon_{\rm i} = 0 & \mbox{for} & E \le E_{\rm g} \quad \mbox{or} \quad E \ge E_{\rm h}
\end{array}
$$
where \({\cal C}_{\rm N}\) is normalization constant. Real part of dielectric function is expressed analyticlally using the Kramers-Kronig relation.
attributes
-
number_of_terms - Adds terms and corresponding parameters (\(N_2\), \(E_2\), \(B_2\), ...).
Example
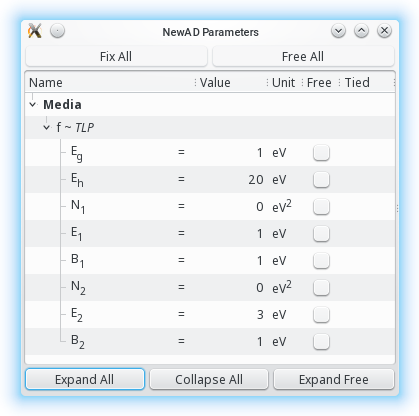
media:
f = TLP:2
newAD2> par
Egf = 2 fixed (0,inf) eV
Ehf = 20 fixed (Egf,inf) eV
N1f = 0 fixed [0,inf) eV2
E1f = 3 fixed (0,inf) eV
B1f = 1 fixed (0,inf) eV
N2f = 0 fixed [0,inf) eV2
E2f = 3 fixed (0,inf) eV
B2f = 1 fixed (0,inf) eV
newAD2>

 |
|