newAD2 - optical characterization software

Gaussian peak

modelname

Gaussian|Gauss|GBP

Complex dielectric function is described by three parameters \(N_1, E_1, B_1\): $$ \varepsilon_\mathrm{r} = 1 + \frac{N_1\sqrt{2}}{\pi B_1 E_1} \left[ \mathrm{D}\!\left( \frac{E+E_1}{\sqrt{2} B_1} \right) - \mathrm{D}\!\left( \frac{E-E_1}{\sqrt{2} B_1} \right) \right] $$ $$ \varepsilon_\mathrm{i} = \frac{N_1}{\sqrt{2 \pi} B_1 E_1 } \left[ \exp\left(-\frac{(E-E_1)^2}{2 B_1^2}\right) - \exp\left(-\frac{(E+E_1)^2}{2 B_1^2}\right) \right] $$ where \(\mathrm{D}\) is special function (Dawson integral). Model represents Gaussian ε-broadened discrete spectrum.

attributes

• number_of_terms - Adds terms and corresponding parameters.
• FWHM - Change meaning of broadening parameters \(B_1, \dots\) from RMS to FWHM, i.e. \(B_1\to B_1/(2\sqrt{2\ln2})\).
• Asymmetric|A - Add parameters \(M2, \dots\) defining asymmetrical peaks (number of peaks must be higher than 1). Appropriate for modelling of coupled phonon peaks.
• Fano|F - Add parameters \(M1, \dots\) defining asymmetrical peaks. Appropriate for modelling of Fano resonace between phonon and free carriers.
• ph - Units 1/cm are used for peak energies \(E_1, \dots\) and broadening parameters \(B_1, \dots\).

Example

media:
  f = Gauss

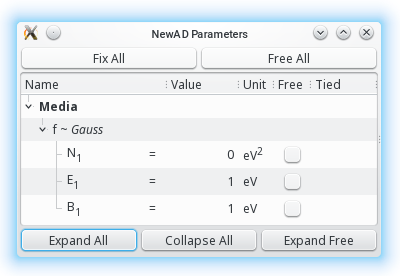
newAD2> par
N1f = 0          fixed [0,inf) eV2
E1f = 1          fixed (0,inf) eV
B1f = 1          fixed (0,inf) eV
newAD2>