Pro správné zobrazení těchto stránek vypněte si, prosím, AdBlock (na stránkách nejsou reklamy).
Tauc-Lorentzův disperzní model
modelname
Tauc-Lorentz|TL
Imaginární část dielektrické funkce je popsána čtyřmi parametry \(E_\mathrm{g}, N_1, E_1, B_1\).
TL model může být počítán pěti různými parametrizacemi, viz. atributy
CC,
JM,
DF1,
ASF a
DF2.
V případě, že není zvolen jeden z atributů, vygenerují se dodatečné čtyři parametry, tj.
\(f_{\rm JM}\), \(f_{\rm CC}\), \(f_{\rm DF1}\), \(f_{\rm DF2}\).
Dielektrická funkce se potom počítá jako lineární kombinace všech verzí Tauc-Lorentzova modelu:
$$
\begin{array}{l}
\hat\varepsilon(E) = 1 + f_{\rm DF2} \ \hat\chi_{\rm DF2}(E) + (1-f_{\rm DF2}) \\
\times \Bigg( f_{\rm CC} \ \hat\chi_{\rm CC}(E) + (1-f_{\rm CC}) \Big( f_{\rm DF1} \ \hat\chi_{\rm DF1}(E) + (1-f_{\rm DF1})
\big( f_{\rm JM} \hat\chi_{\rm JM}(E) + (1-f_{\rm JM}) \, \hat\chi_{\rm ASF}(E) \big)\Big) \Bigg)
\end{array}
$$
kde \(\hat\chi\) jsou odpovídající susceptibility.
atributy
-
CC - Campi-Coriassova verze TL modelu:
$$
\begin{array}{lcl}
\displaystyle
\varepsilon_\mathrm{i} = \frac{2}{\pi} \frac{N_1 B_1 (E-E_\mathrm{g})^2}{E(((E-E_\mathrm{g})^2-(E_1-E_\mathrm{g})^2)^2+B_1^2 (E-E_\mathrm{g})^2)} & \mathrm{for} & E > E_\mathrm{g} \\
\varepsilon_\mathrm{i} = 0 & \mathrm{for} & E \leq E_\mathrm{g}
\end{array}
$$
Reálná část dielektrické funkce je vyjádřena analyticky pomocí Kramers-Kronigovy relace.
-
JM - Jellison-Modinova verze TL modelu:
$$
\begin{array}{lcl}
\displaystyle
\varepsilon_\mathrm{i} = \frac{N_1(E-E_\mathrm{g})^2}{{\cal C}_\mathrm{N} E ((E^2-E_1^2)^2+B_1^2 E^2)} & \mathrm{for} & E > E_\mathrm{g} \\
\varepsilon_\mathrm{i} = 0 & \mathrm{for} & E \leq E_\mathrm{g}
\end{array}
$$
kde \({\cal C}_\mathrm{N}\) je normalizační konstanta. Reálná část dielektrické funkce je vyjádřena analyticky pomocí Kramers-Kronigovy relace.
-
DF1 - Naše první verze TL modelu:
$$
\begin{array}{lcl}
\displaystyle
\varepsilon_\mathrm{i} = \frac{N_1 (E - E_\mathrm{g})^2}{{\cal C}_\mathrm{N}E^3((E-\sqrt{E_1^2-B_1^2/4})^2+B_1^2/4)} & \mathrm{for} & E > E_\mathrm{g} \\
\varepsilon_\mathrm{i} = 0 & \mathrm{for} & E \leq E_\mathrm{g}
\end{array}
$$
kde \({\cal C}_\mathrm{N}\) je normalizační konstanta. Reálná část dielektrické funkce je vyjádřena analyticky pomocí Kramers-Kronigovy relace.
-
ASF - A.S. Ferlauto at al. verze TL modelu:
$$
\begin{array}{lcl}
\displaystyle
\varepsilon_\mathrm{i} = \frac{N_1 \, E \, (E-E_\mathrm{g})^2}{{\cal C}_\mathrm{N} ((E-E_\mathrm{g})^2 + E_\mathrm{p}^2) \,
((E^2-E_1^2)^2+B_1^2 E^2)} & \mathrm{for} & E > E_\mathrm{g} \\
\varepsilon_\mathrm{i} = 0 & \mathrm{for} & E \leq E_\mathrm{g}
\end{array}
$$
kde \({\cal C}_\mathrm{N}\) je normalizační konstanta. Tato parametrizace má jeden extra parameter \(E_\mathrm{p}\),
který ovlivňuje poměr síly přechodu ležící pod a nad energií píku..
Reálná část dielektrické funkce je vyjádřena analyticky pomocí Kramers-Kronigovy relace.
-
DF2 - Naše druhá verze TL modelu:
$$
\begin{array}{lcl}
\displaystyle
\varepsilon_\mathrm{i} = \frac{N_1 (E - E_\mathrm{g})^2}{{\cal C}_\mathrm{N}E((E-E_\mathrm{g})^2 + E_\mathrm{p}^2)((E-\sqrt{E_1^2-B_1^2/4})^2+B_1^2/4)} & \mathrm{for} & E > E_\mathrm{g} \\
\varepsilon_\mathrm{i} = 0 & \mathrm{for} & E \leq E_\mathrm{g}
\end{array}
$$
kde \({\cal C}_\mathrm{N}\) je normalizační konstanta. Reálná část dielektrické funkce je vyjádřena analyticky pomocí Kramers-Kronigovy relace.
-
CJF - Lineární kombinace CC, JM a DF1 verze TL modelu:
$$
\hat\varepsilon(E) = 1 + f_{\rm CC} \ \hat\chi_{\rm CC}(E) + (1-f_{\rm CC}) \Big( f_{\rm JM} \ \hat\chi_{\rm JM}(E) + (1-f_{\rm JM}) \, \hat\chi_{\rm DF1}(E) \Big) .
$$
-
number_of_terms - Přidá další členy a odpovídající parametry \(N_2, E_2, B_2, \dots\).
Příklad
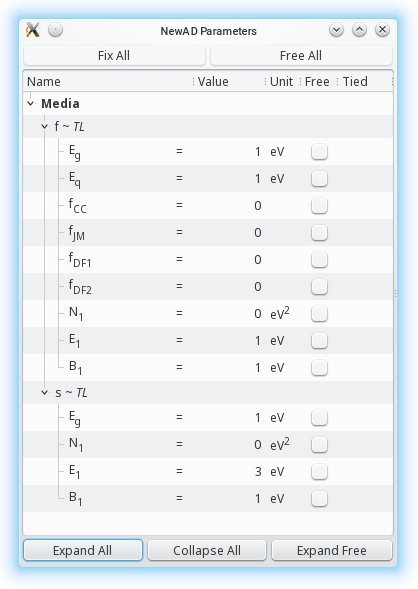
media:
f = TL
s = TL:CC
newAD2> par
Egf = 1 fixed (0,inf) eV
Eqf = 1 fixed (0,inf) eV
fCCf = 0 fixed [0,1]
fJMf = 0 fixed [0,1]
fDF1f = 0 fixed [0,1]
fDF2f = 0 fixed [0,1]
N1f = 0 fixed [0,inf) eV2
E1f = 3 fixed (1e-4,inf) eV
B1f = 1 fixed (1e-4,inf) eV
Egs = 1 fixed (0,inf) eV
N1s = 0 fixed [0,inf) eV2
E1s = 3 fixed (1e-4,inf) eV
B1s = 1 fixed (1e-4,inf) eV
newAD2>

 |
|