Pro správné zobrazení těchto stránek vypněte si, prosím, AdBlock (na stránkách nejsou reklamy).
Rozšířená polynominální funkce
modelname
Poly|Polynominal|Polynom
Nerozšířená imaginární část dielektrické funkce je popsána polynominální funkcí stupně \(K\) mezi minimální
energií \(E_{\rm l}\) a maxímální energií \(E_{\rm u}\)
:
$$
\begin{array}{lcl} \displaystyle
\varepsilon_{\rm i}(E) = N \sum_{n=0}^{K} A_n \left( \frac{E}{E_{\rm u}+E_{\rm l}} \right)^n & \mbox{for} & E_{\rm u} > E > E_{\rm l} \\
\varepsilon_{\rm i}(E) = 0 & \mbox{for} & E \le E_{\rm l} \quad \mbox{or} \quad E \ge E_{\rm u}
\end{array}
$$
kde \(N\) je parametr síly přechodu. \(A_1, A_2,\dots\) jsou parametry definující tvar polynominální funkce (\(A_0\) není volný parametr).
Parametr \(A_0\) je takový, aby platil následující sumační integrál
$$
\int_0^\infty E \varepsilon_{\rm i}(E) \, {\rm d}E = N .
$$
atributy
-
order_of_polynom - Definuje řád polynomu.
-
Lorentz - Lorentzovské rozšíření.
-
Gauss - Gaussovské rozšíření (výchozí).
-
FWHM - V případě gaussovského rozšíření je parametr \(B\) FWHM místo RMS.
-
ph - Pro \(E_{\rm l}\) a \(E_{\rm u}\) použije reciproké centimetry místo jednotek eV.
Příklad
media:
f = Poly:2
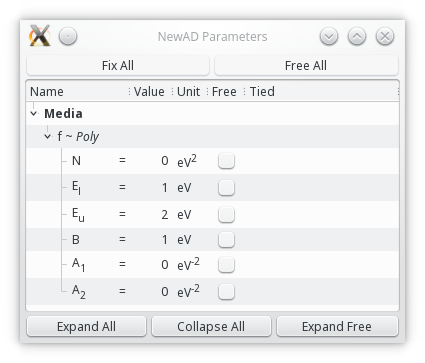
newAD2> par
Nf = 0 fixed [0,inf) eV2
Elf = 1 fixed (0,inf) eV
Euf = 2 fixed (Elf,inf) eV
Bf = 1 fixed (0,inf) eV
A1f = 0 fixed (-inf,inf) eV-2
A2f = 0 fixed (-inf,inf) eV-2
newAD2>

 |
|