newAD2 - program pro optickou charakterizaci

Gaussovský pík

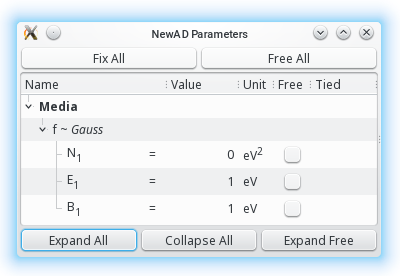
modelname

Gaussian|Gauss|GBP

Komplexní dielektrická funkce je popsána třemi parametry \(N_1, E_1, B_1\): $$ \varepsilon_\mathrm{r} = 1 + \frac{N_1\sqrt{2}}{\pi B_1 E_1} \left[ \mathrm{D}\!\left( \frac{E+E_1}{\sqrt{2} B_1} \right) - \mathrm{D}\!\left( \frac{E-E_1}{\sqrt{2} B_1} \right) \right] $$ $$ \varepsilon_\mathrm{i} = \frac{N_1}{\sqrt{2 \pi} B_1 E_1 } \left[ \exp\left(-\frac{(E-E_1)^2}{2 B_1^2}\right) - \exp\left(-\frac{(E+E_1)^2}{2 B_1^2}\right) \right] $$ kde \(\mathrm{D}\) je speciální funkce (Dawsonův integrál). Model representuje gaussovsky ε-rozšířené diskrétní spektrum.

atributy

• number_of_terms - Přidá další členy a odpovídající parametry.
• FWHM - Změní význam rozširovacích parametrů \(B_1, \dots\) z RMS na FWHM, tj. \(B_1\to B_1/(2\sqrt{2\ln2})\).
• Asymmetric|A - Přidá parametry \(M2, \dots\) definující asymetrické píky (počet píků musí být větší než 1). Vhodné pro modelování vázaných fononových píků.
• Fano|F - Přidá parametry \(M1, \dots\) definující asymetrické píky. Vhodné pro modelování Fano rezonance mezi fonony a volnými nositely.
• ph - Jednotky 1/cm jsou použity pro parametry energie \(E_1, \dots\) a rozšíření píků \(B_1, \dots\).

Příklad

media:
  f = Gauss

newAD2> par
N1f = 0          fixed [0,inf) eV2
E1f = 1          fixed (0,inf) eV
B1f = 1          fixed (0,inf) eV
newAD2>