Pro správné zobrazení těchto stránek vypněte si, prosím, AdBlock (na stránkách nejsou reklamy).
Gauss-Lorentzovský pík
modelname
Gauss-Lorentz|GL
Komplexní dielektrická funkce je popsána čtyřmi parametry jako Voigtovsky rozšířený pík \(N_1, E_1, B_1, L_1\):
$$
\hat\varepsilon = (1-L_1) \hat\varepsilon_{\rm G} + L_1 \hat\varepsilon_{\rm L}
$$
kde imaginární část dielektrické funkce gausovkého a lorentzovského píku je parametrizována dvěma způsoby. První kombinuje píky se stejnou FWHM hodnotou:
$$
\varepsilon_\mathrm{i,G} = \frac{N_1}{\sqrt{\pi} b B_1 E_1 } \left[ \exp\left(-\frac{4\log(2)(E-E_1)^2}{B_1^2}\right) - \exp\left(-\frac{4\log(2)(E+E_1)^2}{B_1^2}\right) \right]
$$
$$
\varepsilon_\mathrm{i,L} = \frac{b B_1}{\pi E_1} \left[ \frac{1}{(E-E_1)^2 + B_1^2/4} - \frac{1}{(E+E_1)^2 + B_1^2/4} \right]
$$
nebo alternativně kombinuje píky se stejným zakřivením v maximech:
$$
\varepsilon_\mathrm{i,G} = \frac{N_1}{\sqrt{\pi} b B_1 E_1 } \left[ \exp\left(-\frac{(E-E_1)^2}{(b B_1)^2}\right) - \exp\left(-\frac{(E+E_1)^2}{(b B_1)^2}\right) \right]
$$
$$
\varepsilon_\mathrm{i,L} = \frac{b B_1}{\pi E_1} \left[ \frac{1}{(E-E_1)^2 + (b B_1)^2} - \frac{1}{(E+E_1)^2 + (b B_1)^2} \right]
$$
kde \(b\) zajiťuje konstantní šířku píku (\(B_1\) je FWHM):
$$
b= \frac{L_1}{2}+\frac{1- L_1}{2 \sqrt{\ln2}} + \sum_{j=1}^4 a_j L_1^j (1- L_1)
$$
\(a_1=0.0552077\), \(a_2=0.0435994\), \(a_3=0.0187772\), \(a_4=0.051632\).
atributy
-
number_of_terms - Přidá další píky a odpovídající parametry.
-
Asymmetric|A - Přidá parametry \(M2, \dots\) definující asymetrické píky (počet píků musí být větší než 1). Vhodné pro modelování vázaných fononových píků.
-
Fano|F - Přidá parametry \(M1, \dots\) definující asymetrické píky. Vhodné pro modelování Fano rezonance mezi fonony a volnými nositely.
-
ph - Jednotky 1/cm jsou použity pro parametry energie \(E_1, \dots\) a rozšíření píků \(B_1, \dots\).
-
Head|H - Použije alternativní výpočet.
Příklad
media:
f = Gauss-Lorentz
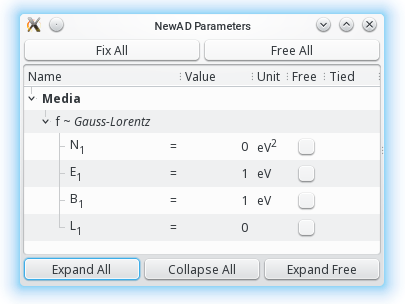
newAD2> par
N1f = 0 fixed [0,inf) eV2
E1f = 1 fixed (0,inf) eV
B1f = 1 fixed (0,inf) eV
L1f = 0 fixed [0,1]
newAD2>

 |
|